Introduction
In this documentation we describe the simulated version of the IQM QPUs available on the Qaptiva. The respective modules come with two main building blocks:
The QPU objects which correspond to the simulated version of the real IQM QPUs
The transpilers which transform general quantum circuits into a form which can run on the IQM QPUs with the respective hardware restrictions (topology, native gate set)
Here it is important that the QPU objects can only handle quantum circuits which satisfy the hardware requirements. Therefore you have two options, either to provide circuits which are already adapted to the hardware restrictions (e.g. by using an external transpiler), or to use the built-in transpilers and run them before the QPU. There is also a stack included in the code, which already combines the transpiler with the QPU, which can be used to execute general circuits with the IQM QPUs. The simulated IQM QPUs contain the actual IQM hardware parameters and return results pretty close to what you would get when running a circuit on the real hardware. Therefore they can be used for various purposes, e.g. to check if you get a reasonable result out compared to the real hardware, if the circuit depth is too high, use case evaluation, etc.
The simulated IQM QPUs
The IQM 5 qubit QPU
One of the QPU objects provided in our module is a simulated 5 qubit version of an IQM QPU. This QPU object expects a quantum circuit with up to 5 qubits as an input and returns the expected measurement result by the respective 5 qubit QPU as an output. It can be seen as a digital twin of the real 5 qubit hardware. The simulated QPU itself consists of a powerful quantum circuit simulator combined with a noise model that describes how the circuits are executed in the noisy environment, i.e. includes noise channels acting while the gates are applied, idle noise, etc. To get a realistic model, the parameters (e.g. gate fidelity, coherence times, etc.) used for the simulation are actual noise parameters published in a git repository by IQM (IQM repository). The parameters are distinct for every qubit to get the most realistic results. Averaged noise parameters are also available; those can be used, e.g., to study the performance of the QPU in general, independent of the qubit mapping.
To use the QPU object in the Qaptiva framework directly on the server you can import the QPU from the qat.qpus module:
from qat.qpus import IQM5SimQPU
If you do not have direct access to the server you can import the IQM 5 qubit QPU via Qaptiva access:
from qlmaas.qpus import IQM5SimQPU
In both cases the QPU can be used in the same way.
Two different noisy QPUs are available in this software stack: the default noisy simulator available in Qaptiva, NoisyQProc, and the MPO simulator.
NoisyQProc can be run in two modes: deterministic, which is an exact simulation storing the full density matrix describing the state of the qubits, and stochastic, which uses stochastic sampling of the final result, thereby reducing memory requirements, at the cost of having intrinsic statistical uncertainty and increasing simulation time. Deterministic NoisyQProc is the default QPU:
iqm_qpu = IQM5SimQPU()
On the Q-Exa Qaptiva, the deterministic mode can only be used up to 18 qubits; to simulate 19 or 20 noisy qubits, one of the approximate simulators (stochastic or MPO) has to be used. If a circuit actually uses less qubits than allocated, the Remap plugin can be used to reduce the memory requirements, allowing circuits with 20 allocated qubits (of which up to 18 can be used) to be run in deterministic mode. The Remap plugin is integrated in the simulated IQM QPUs and can be activated using a parameter, see IQM QPUs. For details on the plugin itself see qat.plugins.Remap in the Qaptiva documentation.
The stochastic mode can be selected as follows:
iqm_qpu = IQM5SimQPU(sim_method='stochastic')
MPO is a Matrix Product Operator based tensor network quantum simulator which can be used to efficiently simulate lowly entangled states. The density matrix of a quantum state of N qubits is cast into a factorized form of N tensors connected to each other with what is generally called bond dimension which can be thought of as the amount of entanglement a quantum state can contain. The standard density matrix representation of the quantum state can then be obtained back by contracting the tensors along the bond dimensions. The main advantage of this representation is that large quantum states can be approximated in a compact way by truncating bond dimensions. This is usually done by limiting bond dimension growth up to a pre-defined maximum bond dimension, which approximates the quantum state. The truncation error grows with the entanglement, therefore limiting MPO to states with low entanglement which can, however, be quite large.
Another option specific to Qaptiva is entanglement-aware MPO (EA-MPO) which dynamically adapts the bond dimensions throughout the simulation based on an input fidelity the quantum state has to reach. The lower the required fidelity is, the more aggressive the algorithm will be at truncating bond dimensions. As noise tends to destroy quantum coherence, EA-MPO is especially useful for simulating highly noisy quantum systems by adapting the bond dimensions to the local entanglement needs throughout the simulation.
The regular MPO QPU using an explicit bond dimension can be instantiated as follows, where X is the required bond dimension:
iqm_qpu = IQM5SimQPU(sim_method='MPO', bond_dimension=X)
The EA-MPO QPU can be instantiated as follows, where X is the required fidelity:
iqm_qpu = IQM5SimQPU(sim_method='MPO', fidelity=X)
The following line of code produces a noiseless version of the QPU (a 5 qubit QPU with the same restrictions on topology and gateset as the real QPU, but no noise):
iqm_qpu = IQM5SimQPU(use_noisy = False)
The noiseless version can for example be used to determine the fidelity of the noisy circuit execution, by comparing the results of both QPU versions.
Once the QPU is initialized, you can define a quantum circuit and execute it analogous to the standard simulators provided in the Qaptiva framework (e.g. LinAlg, NoisyQProc), which is described in detail in IQM QPUs. The resulting object includes all the information resulting from the execution of the job, especially the measurement probabilites for the finally measured state (in logical qubit Z basis). For more information on the result object we refer to the Qaptiva documentation (see qat.core.Result object in Qaptiva documentation)
result = iqm_qpu.submit(iqm_job)
It is important to notice, that all versions of the simulated IQM QPUs act like a real hardware backend, i.e. the provided input circuits must already be adapted to the hardware requirements (topology, native gate set). Otherwise, the QPU is not able to run the job, just like a real QPU. For this purpose, we provide a transpiler plugin which maps a general quantum circuit to a quantum circuit executable on the IQM hardware. This is described in the section Transpilers.
Additionally we provide an iqm_stack object which interconnects our transpiler with the QPU object to create a stack which can take arbitrary input circuits. It can be imported and used in the same way as the IQM QPUs, but is able to take an arbitrary quantum circuit as input which does not match the topology and native gate set restrictions of the QPU. The only requirement that has to be satisfied is the number of qubits. The stack can be instantiated like this:
from qat.qpus import IQM5SimStack
# Create job from quantum circuit NOT adapted to IQM hardware restrictions
general_quantum_job = general_5qubit_circuit.to_job()
iqm_stack = IQM5SimStack()
result = iqm_qpu.submit(general_quantum_job)
A detailed description on how to use the IQM Stacks can be found in IQM Stacks. In addition to the input parameters intended for the QPU the stack supports additional input parameters which define different transpiler modes. The specification of these parameters can be found in section Transpilers.
The IQM 20 qubit QPU
The 20 qubit version of the simulated IQM QPU works in the same manner as the 5 qubit version. The main difference is the number of qubits and the topology included in the QPU. To execute a 20 qubit circuit on this QPU, you can use the same syntax as for the IQM 5 qubit QPU:
from qat.qpus import IQM20SimQPU
iqm_qpu = IQM20SimQPU()
result = iqm_qpu.submit(iqm_job)
There is also an IQM 20 qubit stack which already includes the transpiler and can execute general circuits:
from qat.qpus import IQM20SimStack
# Create job from quantum circuit NOT adapted to IQM hardware restrictions
general_quantum_job = general_20qubit_circuit.to_job()
iqm_stack = IQM20Stack()
result = iqm_qpu.submit(general_quantum_job)
Both the IQM20QPU and the IQM20Stack can be imported via qlmaas analog to the 5 qubit case. The parameters for the 20 qubit simulated version are values measured on the Q-Exa QPU provided by IQM and are available qubitwise as well as averaged.
Transpilers
IQM Transpiler
The following section highlights the key features of the transpiler used to transform arbitrary input circuits to circuits matching the hardware requirements of the IQM QPUs. There are three different versions of the transpiler: the standard PRX transpiler, the optimized VZ transpiler, and a transpiler based on Qaptiva’s default NISQCompiler. In a first step, a pretranspiler is applied which mainly expands three-qubit gates so that only one- and two-qubit gates remain in the circuit. If the PRX or VZ transpiler is used, the Toffoli gate is being transpiled as follows:
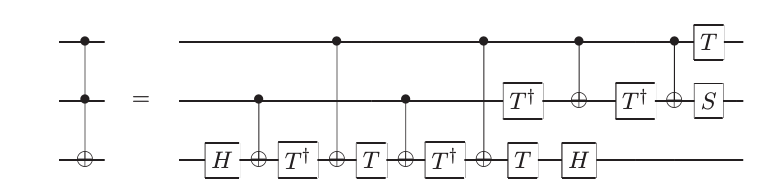
The NISQCompiler uses Qaptiva’s default decomposition of the Toffoli gate.
Afterwards, a topology adaption is performed either via the Nnizer or LazySynthesis method. The Nnizer is used to adapt any arbitrary circuit to the hardware topology by inserting SWAP gates. LazySynthesis on the other hand iterates through the input circuit and differentiates between Clifford and non-Clifford gates, where the “Clifford part” of the circuit is computed classically in a separate step. This can reduce the depth of the circuit considerably but might not be the best option for all input circuits. Please refer to qat.core.LazySynthesis in the Qaptiva documentation for more information. Note that if you are using LazySythesis, the full number of qubits available on the respective QPU needs to be allocated in your circuit, even if not all qubits are actually used, and you may need to post-process your results if you do not run all parts of the calculation in a single pass of the Qaptiva execution stack. There are dedicated stacks to support post-processing; for details see Postprocessing Stacks.
Finally, the circuit is being transpiled into the final IQM gateset, where you have the option to choose between the three transpiler versions mentioned above. By using the PRX transpiler, the gates that are not part of the actual physical gateset of the QPU (the two gates \(PRX\) and \(CSIGN\)) are being transformed accordingly. For instance, the Hadamard gate will be represented (up to a global phase) as two \(PRX\) gates:
where the single-qubit gate \(PRX\) is defined as
The PRX transpiler doesn’t include circuit optimization steps, leaving the transpiled circuit as close to the original circuit as possible. If you prefer to use an optimizing transpiler you should use the VZ transpiler or the NISQCompiler instead.
The VZ transpiler builds on the concept of using virtual Z rotations, which do not have to be executed physically on the QPU and can therefore be considered as being noise-free and instantaneous, to improve the quality of the measurement results (see this paper). Its target gateset consists of the three gates \(PRX\), \(CSIGN\) and (virtual) \(R_Z\). Besides, the VZ transpiler uses an additional optimization method called KAK compression, in which a sequence of one-qubit gates is first merged into one unitary gate and afterwards decomposed into a defined sequence of rotation gates (in our case \(R_ZR_XR_Z\)). This way the total number of \(PRX\) gates within the transpiled circuit can potentially be reduced when compared to using the standard PRX transpiler. Note, however, that this method does not guarantee a reduction of the circuit depth! A more thorough description of the KAK compression method can be found in the Qaptiva documentation (see qat.plugins.KAKCompression in Qaptiva documentation).
The transpiler based on Qaptiva’s NISQCompiler is quite similar to the VZ transpiler. It uses an intermediate gateset consisting of \(CSIGN\), \(R_X(\frac{\pi}{2})\) and \(R_Z\), which is mapped to the native gateset of the QPU in a later transpiler stage, and a KAK decomposition of \(R_Z(\beta)R_X(\frac{\pi}{2})R_Z(\gamma)R_X(\frac{\pi}{2})R_Z(\delta)\). Due to this KAK decomposition it might in general be somewhat less efficient in reducing the single qubit gate count compared to the VZ transpiler; however it generates only \(R_X(\frac{\pi}{2})\) gates (compared to general \(R_X\) gates of any angle) which might be an advantage in some cases.
As mentioned above, the transpiler is already integrated in the IQM Stacks modules. However, it is also possible to call the transpiler separately using the IQM Transpiler. Examples of how to use this plugin can be found in this section as well.
In summary, the transpilation pattern of the PRX and VZ transpiler looks as follows:
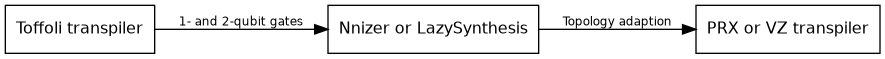
Transpilation procedure for a given input circuit
The NISQCompiler contains the decomposition of Toffoli gates and the topology adaptation as integrated steps.
IQM Observable Splitter
For the execution of observable jobs, one needs to be careful regarding the restrictions given by a real QPU. In particular, the real IQM QPUs are only able to measure in the Z basis, whereas a general observable job needs a measurement in all Pauli basis. Therefore it is necessary to use an additional plugin when sending observable jobs to the real IQM QPUs. This plugin is called IQMObservableSplitter. It converts a general observable job into an observable job which is executable on the IQM QPUs. On the simulated IQM QPUs the observable splitter can also be used but is not required. More details on the plugin can be found in IQM Observable Splitter.